![學習曲線[在一定時間內獲得的技能或知識的速率]](/img/9/cf0/nBnauM3XxAjM1czM0gTMxcTO1UTM1QDN5MjM5ADMwAjMwUzL4EzL1AzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg "學習曲線[在一定時間內獲得的技能或知識的速率]")
簡介
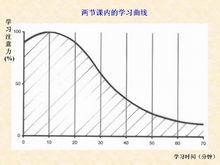
學習曲線learning curve 以橫軸表示反覆次數（探索次數）。以縱軸表示各種學習測試的學習過程的曲線。作為學習測試，在用錯誤數、時間、反應潛時等情況下的負加速下降曲線，如果用正反應數或正反應率為縱坐標。則呈S型或負加速的上升曲線。然而這些曲線型。不僅表示學習效果的增減。而且根據測試的特性，多依賴於理論的界限、生理或行為的界限。另外，把直到學習成功所需的反覆探索數並不相同的許多個體資料，簡單地取反覆探索次數的平均值來表示，則難以表示學習過程的特徵，導致錯誤的結論。所以提出了將學習開始和完成時期劃齊，即用各個體的橫軸或伸或縮，將曲線加合起來的方法。這樣得到的平均曲線稱為奮森曲線（Vincent curve），但幾乎無人使用，不過對從個體所得到的資料還是受重視的。
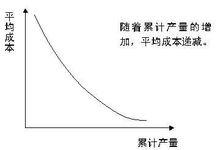
學習曲線也稱為經驗曲線，是隨著產品累計產量的增加，單位產品的成本會以一定的比例下降。學習曲線(Learning curve)是表示單位產品生產時間與所生產的產品總數量之間的關係的一條曲線。
熟練工程，也稱動態評價技術。他們對縮短工時進行動態評價的技術，廣泛套用於生產領域中。
學習曲線將學習效果數量化繪製於坐標紙上，橫軸代表練習次數（或產量），縱軸代表學習的效果（單位產品所耗時間），這樣繪製出的一條曲線，就是學習曲線。
學習曲線有廣義和狹義之分。狹義的學習曲線又稱為人員學習曲線，它是指直接作業人員個人的學習曲線。廣義的學習曲線也稱為生產進步函式，是指工業某一行業或某一產品在其產品壽命周期的學習曲線，是融合技術進步、管理水平提高等許多人努力的學習曲線。
學習曲線是在飛機製造業中首先發現的，利用數據和資料為企業經營管理工作提供預測和決策依據的一種方法，是引起非線性成本的一個重要原因。美國康乃爾大學的商特博士總結飛機製造經驗而得出了學習曲線規律，認為每當飛機的產量積累增加1倍時，平均單位工時就下降約20%，即下降到產量加倍前的80%。商特則將累積平均工時與產量的函式稱為“學習曲線”。
學習曲線體現了熟能生巧。學習曲線是分析採購成本、實施採購降價的一個重要工具和手段。學習帶來成本的降低，其原因可以歸結為以下因素：
(1)隨著生產經驗的豐富，提高了操作人員的操作速度；
(2)降低報廢率和更正率；
(3)改進了操作程式；
(4)因生產經驗帶來模具設計的改進；
學習曲線(圖2)(5)價值工程和價值分析的套用。
概念
在考慮產能大小的決定時，往往要考慮到學習效應這一決定產能大小的重要因素。所謂學習效應是指當以個人或一個組織重複地做某一產品時，做單位產品所需的時間會隨著產品數量的增加而逐漸減少，然後才趨於穩定。如下圖所示：
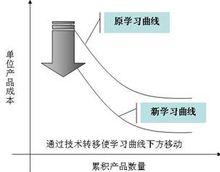
學習效應與學習曲線由上圖可以看出，學習效應包括兩個階段：一是學習階段，單位產品的生產時間隨產品數量的增加逐漸減少；二是標準階段，學習效應可忽略不計，可用標準時間進行生產。上圖中的曲線稱為學習曲線（learning curves）。它所表示的是單位產品的直接勞動時間和累積產量之間的關係。類似的表示學習效應的概念還有“製造進步函式”（manufacturing progress function）和“經驗曲線”（experience curve），但它們所描述的不是單位產品直接勞動時間與累積產量之間的關係，而是單位產品的附加成本與累積數量之間的關係。這兩種曲線的原理與學習曲線是相同的。
常見的學習效應有兩種：個人學習和組織學習。所謂個人學習，是指當一個人重複地做某一產品時，由於動作逐漸熟練，或者逐漸摸索到一些更有效的作業方法後，作一件產品所需的工作時間（即直接勞動時間）會隨著產品累積數量的增加而減少。組織學習是指管理方面的學習，指一個企業在產品設計、工藝設計、自動化水平提高、生產組織以及其他資本投資等方面的經驗累積過程，也是一個不斷改進管理方法，提高人員作業效率的過程。
影響因素
學習曲線(圖3)學習效果受許多因素的影響，主要有：
1）操作者的動作熟練程度。這是影響學習曲線的最基本因素
2）管理技術的改善，正確的培訓、指導，充分的生產準備與周到的服務，工資獎勵及懲罰等管理政策的運用
3）產品設計的改善
4）生產設備與工具的質量
5）各種材料的連續供應和質量
6）信息反饋的及時性
7）專業化分工程度
方程
三個假設
學習曲線(圖5)1）每次完成給定任務或者單位產品後，下一次完成該任務或單位產品的時間將減少；
2）單位產品完成時間將以一種遞減的速度下降；
3）單位產品完成時間的減少將循環一個可以預測的模式。
學習曲線方程的一般形式是:
yx=kxn（n為x的指數）
式中: x=單位數量
yx=生產第x個產品所需的直接勞動小時數
k=生產第一個產品所需的直接勞動小時數
n=lgb/lgx,其中b=學習比例
繪製
學習曲線(圖6)為了繪製一條有用的學習曲線，有許多種對以前數據進行分析的方法。首先我們將按數學程式採用簡單的指數曲線，接著將進行對數分析。在數學制表方法中，一列產品單位數量通過依次倍乘的方式得出，如：1、2、4、8、16……生產第1個單位產品的時間乘以一個學習率得出生產第一、第二件商品的平均時間，生產第1、2個單位產品的時間再乘以一個學習率將得出生產第1~4個單位產品的平均時間時間，依此類推，因此，如果我們繪製一條80%的學習曲線，將得到下表1（80%的學習曲線所需的單位、累計、累計平均值勞動時間）中第2列的數字。為便於計畫通常要知道累計直接勞動時間，下表1（80%的學習曲線所需的單位、累計、累計平均值勞動時間）的第4列也提供了這方面的信息。這些數字的計算比較簡單。
分析
對數分析
學習曲線方程的標準形式是（此方程說明隨著生產數量的增加，任何一個給定單位產品的直接勞動小時數將按指數規律遞減）：
n
Yx=KX
式中：X----單位數量；
Yx---生產第X個產品所需要的直接勞動小時數；
K----生產第一個產品所需要的直接勞動小時數；
n----㏒b/㏒2 其中b為學習率
上述問題我們可經用數學方法解決，好可以用下面的表來解決。
例題：
利用數學方法我們計算上表一中第8個單位產品所需要的勞動時間。
我們利用下式計算：
n
Yx=KX
㏒0.8/㏒2 －0.322 0.322
Y8=100 000×8 =100 000×8 =100 000/8
=100 000/1.9535
=51 192
因此生產第8個產品將需要52 192小時。
學習曲線表
知道學習率後，就可以利用下面給出的表2和表3非常方便的估計出某一特定產品或某一組產品的勞動時間。我們只需要把最初的勞動小時數乘以表中給出的相應值。
方法詳解如下：
假設我們檢查上表1中第16個單位產品的勞動小時數和累計勞動小時數。我們從下表2可以查知，第16個單位產品在80%的學習率下提高係數為0.4096，該數乘以生產第一個單位產品的小時數100 000得到40960，驗證同上表一中給出的完全一樣。從下表3中查知，前16個單位產品的累計提高係數為8.920，同樣乘以生產第一個單位產品的小時間數100 000後得到892000。同上表1中得出的值892014非常接近。
學習率的估計
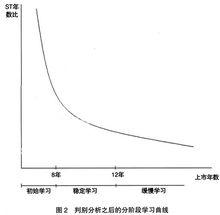
如果已經開始生產了一段時間，通過以前的生產記錄能夠很容易的得到學習率。一般來說，生產時間越長，評估就越準確，因為生產的初期可能發生很多情況，所以大部分的生產公司直到生產了一些產品後才收集用於學習曲線分析的數據。
在估計學習率時還應採用統計分析。採用指數學習曲線可以看出該曲線對以前數據的符合程度。這些數據也可以在對數坐標紙上繪製，以觀察其是否具有直線性。
如果生產還未開始，對學習率的估計就是一個具有啟發性的猜測問題。在這種情況下，分析員有以下三種選擇：
1、假設估計的學習率同以前性質的企業中的學習率一樣；
2、假設估計的學習率與同樣的或類似的產品的學習率是一樣的；
3、分析學習前的運轉方式與前面的運轉方式的相同點和不同點，並由此得出適合此種情況的經過修正的學習率。
套用
學習曲線(圖4)1）在生產製造方面，它可以套用於估計產品設計時間和生產時間，同時可以套用於估計成本；
2）學習曲線也是公司戰略設計的組成部分，比如價格、投資成本和營運成本的決策；
3）套用於個體學習和組織學習的能力。
4）學習曲線如使用不當也是有一定風險的。這是指管理人員往往容易忘記環境動態變化的特性，在這種情況下，環境變化中的不測因素有可能影響學習規律，從而給企業帶來損失。一個著名事例是道格拉斯飛機製造公司被麥克唐納兼併的事例。道格拉斯飛機曾經根據學習曲線估計它的某種新型噴氣式飛機成本能夠降低，於是對顧客許諾了價格和交貨日期，但是飛機在製造過程中不斷地修改工藝，致使學習曲線遭破壞，也未能實現成本降低，因此遇到了嚴重的財務危機，不得不被兼併。
學習曲線法則是指在一個合理的時間段內，連續進行有固定模式的重複工作，工作效率會按照一定的比率遞增，從而使單位任務量耗時呈現一條向下的曲線。學習曲線效應是在以下兩種因素的共同作用下產生的：一是熟能生巧，連續進行有固定套路的工作，操作會越來越熟練，完成單位任務量的工作時間會越來越短；二是規模效應，生產10件產品與100件產品所需要的生產準備時間、各生產環節間的轉換時間是一樣的，因此一次生產的產品越多，分攤到每件產品上的準備時間和轉換時間越少，單位生產效率越高。
學習曲線法則告訴我們，應儘量集中處理性質相同的事務性工作， 如一次性處理具有相同性質的所有檔案，一次性打完所有的溝通電話，一次購齊所需的生活用品，一次性做完所有家務等。這樣既有利於提高工作的熟練程度，又能通過批量作業減少準備工作和中間環節占用的時間，從而達到節約時間、提高效率的目的。
例題：
某數碼電子有限公司有一條手動外掛程式生產線，該線有35名員工，手工插14英寸彩色電視機主機板日產量為1200塊，每個主機板的單位生產成本為9元人民幣。生產線管理人員要求，在一個星期內該生產線累計完成10000塊。問每塊主機板的單位生產成本是多少？
如果該生產線的經驗曲線為90%，那么，一星期內該生產線累計完成10000塊主機板的生產成本應該是：9×90%=8.10元人民幣。
學習曲線可通過數學列表、數學對數或其它的一些曲線擬合方法得到，這取決於可利用數據的形式及可利用數據的多少。
從學習曲線考慮，效率的提高有二種方法，既單位產品生產時間學習曲線或單位時間生產量學習曲線。
單位產品生產時間學習曲線給出了每連續生產一件產品所需要的生產時間，累計平均時間曲線給出了產品總數目增加時的累計平均操作時間。單位產品生產時間曲線和累計平均時間曲線也稱為“進步曲線”、“產品學習曲線”，它們對於複雜的產品或生產周期長的產品較適應。單位時間生產量曲線也稱為工業學習曲線，通常用於大量生產（短周期）。
指導
1、個人學習
有許多因素影響個人的表現和學習率。學習率和初始水平是其中最重要的兩個因素。我們假定為了完成一項簡單任務，測試兩個員工生產某件產品的時間，這項測試被行政部用來作為對裝配線上招聘員工考核的一部分。
有兩個人應聘裝配線員工，你將聘用那一個？應聘者A開始效率高但學習速度慢；應聘者B雖然開始效率低，但是他的學習速度很快。很明顯B是一個更好的聘用人。以上說明不僅學習率本身很重要，起始操作時間也很重要。
為了改善個人的操作水平，基於學習曲線的一般指導方針有：
⑴合理選擇員工。應採用某些測試來幫助選擇員工；這些測試對計畫好的工作具有代表性：裝配工作測試其靈巧性，腦力工作測試其腦力勞動能力，服務性工作測度其與顧客溝通的能力等。
⑵合理的培訓。培訓方式越有效，學習率就越高。
⑶激勵。除非有報酬，否則基於學習曲線的生產任務很難完成。
⑷工作專業化。一般的規律是：任務愈簡單，學習的愈快。應注意由於長期操作同一作業所導致的厭煩感是否會對工作產生干擾。如果確實對工作產生了干擾，那么就要對任務進行重新設計。
⑸一次完成一項或很少的作業。對於每一項工作，一次只完成一項比同時做所有的工作學習的快。
⑹使用能夠輔助或支持操作的工具或設備。
⑺能夠提供快速而簡單回響幫助的方法。
⑻讓員工協助重新設計他們的工作。把更多的操作因素考慮到學習曲線的範圍中，實際上能夠使曲線向下傾斜的速度更快。
2、組織學習
組織同樣也在學習，從工業工程（IE）角度考慮組織學習對於企業間的競爭也是關鍵的。對於個人來說，知識如何獲得和保存以及這些將對個人學習產生多大的影響等方面的概念很容易建立。當然組織學習主要源於所有聘用員工個人學習的結果。
例如：隨著操作者越來越熟練，知識就嵌入到軟體和操作方法中去了。知識也可以嵌入到組織的結構中去。如：當一個組織把它的工業工程（IE）團隊從集中於某一地點的功能組織中轉移到員工分散在工廠各地的分權組織中時，怎樣提高生產率這些方面的知識將會嵌入到組織結構中去。
如果個人離開組織，知識將貶值。
如果技術水平達不到或難以使用，知識也會貶值。
例題：
一個求職者正在測試自己能否勝任一條裝配線上的工作，管理部門認為，在操作1000次後就大體上達到了穩定狀態。預計普通裝配員工在4分鐘內完成該任務。
⑴如果求職者第一次操作時間為10分鐘，第二次操作為9分鐘，是否該聘用此求職者？
⑵該求職者第10次操作的預期時間是多少？
解：
⑴學習率=9分鐘/10分鐘=90%
從學習曲線單位提高值表 中查知，第1000次操作要求的時間為0.3499×10分階段鍾=3.449分鐘。因此，該聘用此人。
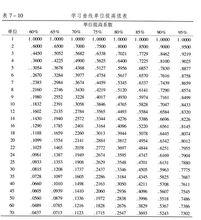學習曲線單位提高值表⑵從學習曲線表單位提高值表 中查知，學習率在90%時，第10次操作的提高係數為0.7047，因此第10次操作時間為0.7047×10=7.047分鐘。
